Question

Aaron invested $570 in an account paying an interest rate of 7% compounded continuously. Assuming no deposits or withdrawals are made, how much money, to the nearest dollar, would be in the account after 8 years?

Answer 1

The amount of money that would be in the account after 8 years is approximately $998

Explanation:

The given parameters for the compound interest investment are;

The amount Aaron invested = $570

The interest rate of the investment = 7%

The mode of compounding of the interest = Continuously

The number of years the amount is invested = 8 years

For a compounded continuously interest rate, we have;

`A = P \cdot e^(r \cdot t)`

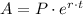
Where;

A = The future value =The amount realized from the investment after the time of investment

P = The initial value = The principal amount invested

e = Euler's number = Mathematical constant

r = The interest rate = 7%

t = The time of investment = 8 years

Therefore, by substituting the known values, we have;

`A = 570 * e^(0.07 * 8) \approx 997.883325`

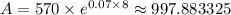
The amount of money that would be in the account after 8 years to the nearest dollar = The future value of the investment = A ≈ 998

The amount of money that would be in the account after 8 years to the nearest dollar ≈ $998.