Question

In an Arithmetic progression,

t15​=30,t20​=50
Find,
S17​=??
​

Answer 1

Question : -

In an Arithmetic progression,
`\sf{t_(15) = 30 \; , t_(20) = 50 }`

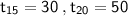
Find S₁₇ ?

Given :-

• t₁₅ = 30; t₂₀ = 50

Required to find : -

• S₁₇=??

Solution : -

Given that;

• t₁₅ = 30; t₂₀ = 50

t₁₅ represents the 15th term of the AP

t₂₀ represents the 20th term of the AP

Now,

We know that;

t₁₅ can be represented as , a + 14d

t₂₀ can be represented as , a + 19d

Now, This implies

• a + 14d = 30 ••••••(1)

• a + 19d = 50 •••••••(2)

Subtract eq 1 from eq 2

a + 19d = 50

a + 14d = 30

(-)(-) (-)

-------------------

0 + 5d = 20

• 5d=20-0
• 5d = 20
• d = (20)/(5)
• d = 4

So,

Common difference (d) = 4

Substituting the value of d in eq-1

• a + 14d = 30
• a + 14(4) = 30
• a + 56 = 30
• a = 30 - 56
• a = -26

So,

First term (a) = -26

Now,

Let's find the sum of first 17 terms !

We know that;

`\tt{S_(n)= (n)/(2)[2a+(n-1)d]}`

Now,

Here the no. of term (n) = 17

We have,

• S₁₇ = (17)/(2) [2(-26)+(17-1)4]
• S₁₇ = (17)/(2) [-52 + (16)4]
• S₁₇ = (17)/(2) [-52 + 64]
• S₁₇ = (17)/(2) [12]
• S₁₇ = (17 x 12)/(2)
• S₁₇ = 17 x 6
• S₁₇ = 108

Therefore,

S₁₇ = 108