Question

the function f(x) = –x2 − 2x 15 is shown on the graph. what are the domain and range of the function? the domain is all real numbers. the range is y < 16. the domain is all real numbers. the range is y ≤ 16. the domain is x. the range is y. the domain is x. the range is y.

Answer 1

The domain is all real numbers.

The range is y ≤ 16

Explanation:

Given function,

`f(x)=-x^2-2x+15`

`f(x) = -x^2 - 2x + 15 + 1 - 1`

`f(x) = -(x^2 + 2x + 1) + 16`

`f(x) = -(x+1)^2 + 16`

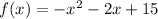
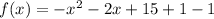
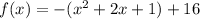
Which a downward parabola,

∵ The vertex form of a parabola is
`f(x)=a(x-h)^2 + k`

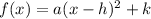
Where, (h, k) is the vertex of the parabola,

Thus, the vertex of the above parabola = ( -1, 16 ),

Since, a downward parabola gives maximum output value on its vertex,

So, the range of the parabola = all real numbers less than equal to 16,

i.e. Range = y,

Now, a parabola is a polynomial and a polynomial is defined for all real numbers,

Hence, Domain = All real numbers

Answer 2

-x^2 - 2x + 15 in vertex form is -(x^2 + 2x - 15) = -(x^2 + 2x + 1 - 16) = -(x + 1)^2 + 16

Therefore, domain is all real numbers and range is y.