Answer:
The correct option is 2.
Explanation:
The given function is
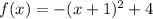 ..... (1)
..... (1)
The standard form of a parabola is
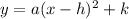 .....(2)
.....(2)
Where, (h,k) is the vertex and a is stretch factor.
On comparing (1) and (2), we get



The vertex of the parabola is (-1,4). Since a=-1<0, therefore it is a downward parabola. Domain of an downward parabola is all real numbers.
The vertex of a downward parabola is the point of maxima. So the range of the function can not be more that 4.
Therefore the domain is all real numbers, and the range is y ≤ 4. Option 2 is correct.