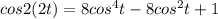Question

Find an identity for cos(4t) in terms of cos(t)?

Answer 1

The question in the problem wants to calculate the identity for  cos(4t) in terms of cos(t) and base on the given and further computation, I would say that the answer would be 2cos^2(2t)-1. I hope you are satisfied with my answer and feel free to ask for more if you have question and further clarification

Answer 2

Find out the cos(4t) in terms of cos(t) .

To prove

As given the identity in the question be cos(4t) .

It is written as

`cos(4t) = cos(2(2t))`

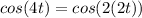
Now using the trignometric formula

`cos2A = 2cos^(2)A - 1`

`cos2(2t) = 2(2cos^(2)t -1)^(2) -1`

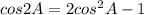
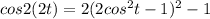
Apply (a +b )² = a² + b² + 2ab

`cos2(2t) = 2(4cos^(4)t - 4cos^(2)t +1) -1`

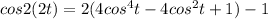
Simplify the above

`cos2(2t) = 8cos^(4)t - 8cos^(2)t +1`

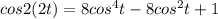
Therefore the expression cos(4t) in terms of cos(t) is

`cos2(2t) = 8cos^(4)t - 8cos^(2)t +1`