Question

Check all that apply: If sin theta = 15/17 then:

a. tan theta = 15/8
b. csc theta = 17/15
c. coc theta = 17/8
d. sec theta = 17/8

Answer 1

`a.tan(\theta)=(15)/(8)`

`b.csc(\theta)=(17)/(15)`

`d.sec(\theta)=(17)/(8)`

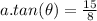
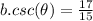
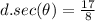
Explanation:

The trigonometry functions on a right triangle are given by:

`sin(\theta)=(opposite)/(hypotenuse)`

`csc(\theta)=(hypotenuse)/(opposite)`

`cos(\theta)=(adjacent)/(hypotenuse)`

`sec(\theta)=(hypotenuse)/(adjacent)`

`tan(\theta)=(opposite)/(adjacent)`

`cot(\theta)=(adjacent)/(opposite)`

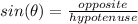
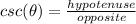
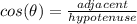
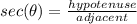
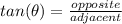
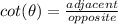
Let's calculate the adjacent side using pythagorean theorem:

`a^2+b^2=c^2`

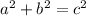
Where:

a=opposite

b=adjacent

c=hypotenuse

The problem provides us a and c because:

`sin(\theta)=(opposite)/(hypotenuse)=(15)/(17)`

So:

`15^2+b^2=17^2`

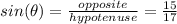
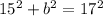
Solving for b:

`b^2=17^2-15^2\\b^2=289-225\\b^2=64\\b=√(64) \\b=8`

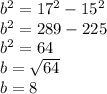
Therefore:

a=opposite=15

b=adjacent=8

c=hypotenuse=17

Finally, let's see if the given options are correct:

`a.tan(\theta)=(15)/(8)=(opposite)/(adjacent)=(15)/(8)` , This is correct.

`b.csc(\theta)=(17)/(15)=(adjacent)/(hypotenuse)=(17)/(15)` , This is correct.

`c.cot(\theta)=(17)/(8)=(adjacent)/(opposite)=(8)/(15)` , This is incorrect.

`d.sec(\theta)=(17)/(8)=(hypotenuse)/(adjacent)=(17)/(8)` , This is correct.