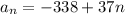Answer:
The nth for the arithmetic sequence is given by:
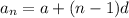 ....[1]
....[1]
where,
a is the first term
d is the common difference of two consecutive terms.
n is the number of terms.
As per the statement:
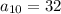 and
and
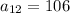
Using [1] we have;
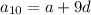
⇒
 ......[2]
......[2]
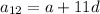
⇒
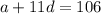 .......[3]
.......[3]
Subtract equation [2] from [3] we have;
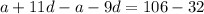
Simplify:
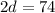
Divide both sides by 2 we get;
d = 37
Substitute the value of d in [2] we have;
a+9(37) = 32
a+333 = 32
Subtract 333 from both sides we have;
a = -301
Then substitute the value a and d in [1] we have;

⇒
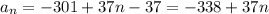
Therefore, an equation for the nth term of the arithmetic sequence is :