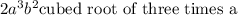Answer:
1. Option D is correct.
2. Option C is correct
Explanation:
1.
Given the statement: four square root of eleven•four square root of ten
"four square root of eleven" translated to
![\sqrt[4]{11}](https://img.qammunity.org/2017/formulas/mathematics/high-school/b5u14wuimunjwku9w58vzxenpjrfbz2glc.png)
"Four square root of ten" translated to
![\sqrt[4]{10}](https://img.qammunity.org/2017/formulas/mathematics/high-school/lik927j6at49zqk6zer351qy8hhximeuuf.png)
then; we have
![\sqrt[4]{11} \cdot \sqrt[4]{10} = \sqrt[4]{11 \cdot 10} =\sqrt[4]{110}](https://img.qammunity.org/2017/formulas/mathematics/high-school/uqtgqtjo4z9kp1bxc812bqm5e6ssx2hngd.png)
Therefore, we get the answer four square root of one hundred ten i.,e
![\sqrt[4]{110}](https://img.qammunity.org/2017/formulas/mathematics/high-school/qld30qket5vjdkyl02m9us4df4irdwq76e.png)
2.
To find the simplest form of the expression.
Given: cubed root of twenty four times a to the tenth times b to the sixth.
This translate to:
![\sqrt[3]{24 \cdot a^(10) \cdot b^6}](https://img.qammunity.org/2017/formulas/mathematics/high-school/8zoqhu5pm193koqrhs48z16lh7cmte16ki.png)
Simplify:
![\sqrt[3]{24 \cdot a^(10) \cdot b^6}](https://img.qammunity.org/2017/formulas/mathematics/high-school/8zoqhu5pm193koqrhs48z16lh7cmte16ki.png)
We know:
![\sqrt[n]{a^n} = a](https://img.qammunity.org/2017/formulas/mathematics/high-school/95efingy24e4sk3ek7zogrk6bpf7zs3wrs.png)
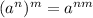
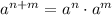
then;
![\sqrt[3]{24 \cdot a^(10) \cdot b^6}](https://img.qammunity.org/2017/formulas/mathematics/high-school/8zoqhu5pm193koqrhs48z16lh7cmte16ki.png)
=
![\sqrt[3]{8 \cdot 3 \cdot a^9 \cdot a \cdot (b^2)^3}](https://img.qammunity.org/2017/formulas/mathematics/high-school/a7c50km84s8fqvn4mosg8mq7cyplkkc4px.png)
=
![\sqrt[3]{2^3 \cdot 3 \cdot (a^3)^3 \cdot a \cdot (b^2)^3}](https://img.qammunity.org/2017/formulas/mathematics/high-school/560xpv4hmg784btu07nmtiq88kx28f2mkp.png)
=
![2 \cdot a^3 \cdot b^2\cdot \sqrt[3]{3 \cdot a}](https://img.qammunity.org/2017/formulas/mathematics/high-school/tmbgble1qth910cqz4n7924bl8kjoxs9yx.png)
or
=
![2a^3b^2\sqrt[3]{3a}](https://img.qammunity.org/2017/formulas/mathematics/high-school/q43b6dgd68ufc1q22n45sdu83xxmqn91s6.png)
Therefore, the simplest form of the given expression is,
![2a^3b^2\sqrt[3]{3a}](https://img.qammunity.org/2017/formulas/mathematics/high-school/q43b6dgd68ufc1q22n45sdu83xxmqn91s6.png) or
or