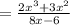Question

Simplify quantity 6 x plus 9 over 15 x squared all over quantity 16 x minus 12 over 10 x to the fourth power

Answer 1

`(6x + 9)/(15x^(2)) / (16x - 12)/(10x^(4))`

`(3(2x) + 3(3))/(3(5x^(2))) / (4(4x) - 4(3))/(2(5x^(4)))`

`(3(2x + 3))/(3(5x^(2))) / (4(4x - 3))/(2(5x^(4)))`

`(2x + 3)/(5x^(2)) / (2(4x - 3))/(5x^(4))`

`(2x + 3)/(5x^(2)) * (5x^(4))/(2(4x - 3))`

`(2x + 3)/(1) * (x^(2))/(2(4x - 3))`

`(2x^(3) + 3x^(2))/(8x - 6)`

Answer 2

Simplify the quantity 6 x plus 9 over 15 x squared all over quantity 16 x minus 12 over 10 x to the fourth power .

To prove

As given

the quantity 6 x plus 9 over 15 x squared all over quantity 16 x minus 12 over 10 x to the fourth power .

Now written this in the simple form

Now simplify the above equation

Now using the property

`(y^(a))/(y^(b)) = y^(a-b)`

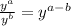
Thus

Now again simplify the above equation

`= (3(2x+3)* 10x^(2))/(15* 4(4x-3))`

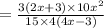
Thus

`= ((2x+3)* x^(2))/(2* (4x-3))`

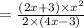
Therefore

`= \frac{2x^(3)+3x^(2)} {8x-6}`