Question

give the standard form, degree, leading coefficient and the constant term of the function h(x) = (2x+1)² (2x-3)​

Answer 1

The standard form is:
`h(x) = 8x^3 - 4x^2 - 10x - 3`

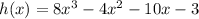
The function is of the 3rd degree.

The leading coefficient is 8.

The constant term is -3.

Explanation:

Placing in standard form:

To place in standard form, we solve the operations. So

`h(x) = (2x+1)^2(2x-3)`

`h(x) = (4x^2 + 4x + 1)(2x - 3)`

`h(x) = 8x^3 - 12x^2 + 8x^2 - 12x + 2x - 3`

`h(x) = 8x^3 - 4x^2 - 10x - 3`

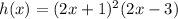
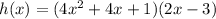
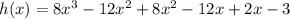
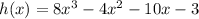
Degree:

The degree is given by the highest power of x, which, in this exercise, is 3.

Leading coefficient:

The leading coefficient is the term that multiplies the highest power of x. In this exercise, the higher power of x is
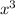`x^3`, which is multiplied by 8. So the leading coefficient is 8.

Constant term:

The constant term is the one which does not multiply a power of x. So in this exercise, it is -3.