Question

Find dy/dx given y = definite integral 1/(1+t^2) . upper cosx. lower 0. show steps/explain.

Answer 1

Hello,

If i have well understood:


`image`

Answer 2

`\displaystyle y' = (-\sin x)/(1 + \cos^2 x)`

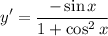
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Integration

• Integrals

Integration Rule [Fundamental Theorem of Calculus 2]:
`\displaystyle (d)/(dx)[\int\limits^x_a {f(t)} \, dt] = f(x)`

Explanation:

Step 1: Define

Identify

`\displaystyle y = \int\limits^(\cos x)_0 {(1)/(1 + t^2)} \, dt`

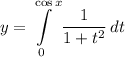
Step 2: Differentiate

1. Chain Rule:
   `\displaystyle y' = (d)/(dx) \bigg[ \int\limits^(\cos x)_0 {(1)/(1 + t^2)} \, dt \bigg] \cdot (d)/(dx)[\cos x]`
2. Fundamental Theorem of Calculus 2:
   `\displaystyle y' = (1)/(1 + \cos^2 x) \cdot (d)/(dx)[\cos x]`
3. Trigonometric Differentiation:
   `\displaystyle y' = (1)/(1 + \cos^2 x) \cdot -\sin x`
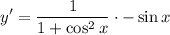
4. Simplify:
   `\displaystyle y' = (-\sin x)/(1 + \cos^2 x)`

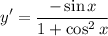
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration