Question

If the world’s population is increasing at an annual rate of 1.3%, and there were 5 billion people in the year 1986, then in what year will the world’s population be 10 billion?

Answer 1

Using the formula for exponential growth with an initial population of 5 billion in 1986 and an annual growth rate of 1.3%, it is calculated that the world's population would reach 10 billion approximately 70 years later, around the year 2056. This assumes a constant growth rate.

Step-by-step explanation:

Calculating Future Population Based on Growth Rate

To determine the year when the world's population will be 10 billion, starting from 5 billion in 1986 with an annual growth rate of 1.3%, we use the formula for exponential growth:

`P(t) = P_0 * (1 + r)^t`

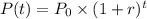
Where:

• P(t) is the future population
• P_0 is the initial population
• r is the annual growth rate
• t is the time in years

Substituting the given values, we have:

`10 billion = 5 \ billion\ * (1 + 0.013)^t`

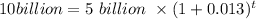
To solve for t, take the logarithm of both sides:

log(10 billion) - log(5 billion) = t × log(1.013)

Dividing by log(1.013) to isolate t:

t = (log(10 billion) - log(5 billion)) / log(1.013)

By calculating, we find that t is approximately 70 years. Adding 70 years to the base year 1986 gives us 2056 as the year the population would reach 10 billion.

Answer 2

5 billion * ( 1 + 0.013 ) ^x = 10 billion
1.013 ^x = 10 : 5 = 2

`x = log_(1.013)2`
x = 54
1986 + 54 = 2040
In the year 2040 the world`s population will be 10 billion.