Answer:
(-4, -4)
Explanation:
A quadratic equation
 has written in vertex form using the completing square method is:
has written in vertex form using the completing square method is:

where, (h, k) is the vertex
As per the statement:

Using the completing square method we have;
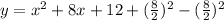
⇒
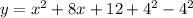
Using identity rule:
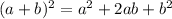
then;
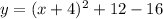
⇒
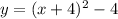
vertex of the given equation is: (h, k) = (-4, -4)
Therefore, the vertex of the parabola whose equation
 is (-4, -4)
is (-4, -4)