Question

In a Quadratic equation


`\sf 4x^2-13x+k=0`

One root of the equation is 12times more than the another root.Find the value of k

Note:-

Answer minimum 45+words​

Answer 1

Question :-

In a Quadratic equation 4x² - 13x + k = 0 , one root of this equation is 12 times more than the another root. Find the value of k.

Given :-

One root of quadratic equation is 12 times more than the another root.

Solution :-

Let , the one root of the quadratic equation is m and the another is n then according to the Question ,

• 
  `\star \sf \: n = 12m - - - - (i)`

Given quadratic equation is 4x² - 13x + k = 0

• Now comparing the given equation by ax² + bc + c = 0,

`\begin{gathered} \star \sf \: a = 4 \\ \\ \star \sf \: b = - 13 \\ \\ \star \sf \: c = k\end{gathered}`

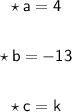
Now , we know that :-

`\sf \: sum \: of \: roots = - (b)/(a)`

So,

`\begin{gathered} \star \sf \: m + n = - (( - 13))/(4) \\ \\ \sf \: substituting \: the \: value \: of \: n \: from \: equation \: (i) \\ \\ \mapsto \sf \: m + 12m = (13)/(4) \\ \\ \mapsto \sf \: 13m = (13)/(4) \\ \\ \mapsto \sf m = (13)/(4 * 13) \\ \\ \mapsto \boxed{ \sf m = (1)/(4) }\end{gathered}`

• Hence the first root of the equation of 1/4 so , the second root is -

`\begin{gathered} \sf \star \: n = 12m \\ \\ \mapsto \sf \: n = 12 * (1)/(4) \\ \\ \mapsto \boxed{\sf n = 3}\end{gathered}`

• So the second root of the quadratic equation is 3.

Now, we know that :-

`\sf \: product \: of \: roots = (c)/(a)`

So,

`\begin{gathered} \star \sf \: m * n = (k)/(4) \\ \\ \mapsto \sf (1)/(4) * 3 = (k)/(4) \\ \\ \mapsto \sf k = (1)/(4) * 4 * 3 \\ \\ \mapsto \boxed{\sf k = 3 }\end{gathered}`

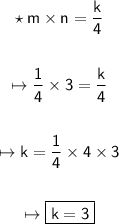
Hence, the value of k is 3.