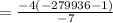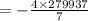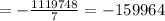Question

What is the sum of the geometric sequence –4, 24, –144, … if there are 7 terms? A) 308,829 B) –159,964 C) –411,772 D) 119,973 .

Answer 1

The sum is -159964.

Explanation:

Since, the sum of a geometric sequence is,

`S_n=(a(1-r^n))/(1-r)\text{ When } |r| < 1`

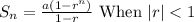
or
`S_n=(a(r^n-1))/(r-1)\text{ When } |r| > 1`

Where, a is the first term of the sequence,

r is the common ratio,

n is the number of terms,

Given, sequence,

–4, 24, –144, …....., up to 7 terms,

Thus, a = - 4

`r=(24)/(-4)=-6`

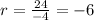
And, n = 7,

Since, |-6| > 1

Therefore, the sum of the given sequence is,

`S_7=(-4((-6)^7-1))/(-6-1)`

`=(-4(-279936-1))/(-7)`

`=-(4* 279937)/(7)`

`=-(1119748)/(7)=-159964`

Answer 2

Sum of the geometric sequence:
S n = a * ( 1- r^n ) / ( 1 - r )
a = - 4 ( the 1st term of the sequence ), r = - 6, n = 7
S 7 = (- 4 ) * ( 1 - ( - 6 )^7 ) / 1 - ( - 6 ) = ( - 4 ) * 279937 / 7 = - 159,964
Answer: B )