Answer:
359,007 cubic feet
Explanations:
1) The formula for calculating the volume of the spherical tank is expressed as:
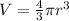
where:
r is the radius of the tank
The volume of the quarter-sphere shaped tank is expressed according to the formula

Substitute the value for the radius as shown below

Therefore the volume of of the quarter-sphere shaped tank to the nearest whole number is 359,007 cubic feet