Question

The spread of a highly contagious virus in a high school can be described by the logistic functiony=72001+799e−0.7xwhere x is the number of days after the virus is identified in the school and y is the total number of people who are infected by the virus.(a) Graph the function for 0≤x≤15.(b) How many students had the virus when it was first discovered?(c) What is the upper limit of the number infected by the virus during this period?

Answer 1

(a) Choosing the correct graph.

`\text{Graphing the function }y=(7200)/(1+799e^(-0.7x))\text{ yields}`

(b) Finding the number of students who had the virus when it was first discovered.

Substitute x = 0 to the logistic function to determine the number of students infected.

`\begin{gathered} y=(7200)/(1+799e^(-0.7x)) \\ \\ \text{If }x=0 \\ y=(7200)/(1+799e^(-0.7(0))) \\ y=(7200)/(1+799e^0) \\ y=(7200)/(1+799(1)) \\ y=(7200)/(800) \\ y=9 \end{gathered}`

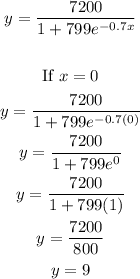
Therefore, there were 9 students who had the virus when it was first discovered.

(c) Upper limit of the number of infected by the virus.

As the number of days increases, the given logistic function of the virus plateaus at y = 7200.

Therefore, the upper limit of the number infected by the virus during this period is 7200.