Question

Does the point (-1, V15) lie on the circle centered at the origin and containing the point (0,4)?Explain.

Answer 1

Step-by-step explanation:

The equation for a circle centered at the origin is:

`x^2+y^2=r^2`

Where r is the radius of the circle.

For this problem it says that it contains point (0, 4). Therefore the radius of the circle is 4 and the equation is:

`\begin{gathered} x^2+y^2=4^2 \\ x^2+y^2=16 \end{gathered}`

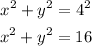
If we replace the given point into the equation and the equality is true, then the point lies on the circle:

`\begin{gathered} (-1)^2+(\sqrt[]{15})^2=16 \\ 1+15=16 \\ 16=16\text{ true} \end{gathered}`

Answer:

Yes, because the equation for the circle is x² + y² = 16 and (-1)² + (√15)² = 16