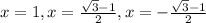A convenient way to find the zeros of
 is by factoring.
is by factoring.
a) The equation,

can be rewritten as,
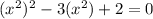
We can think of this equation as a quadratic equation in
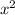 , with
, with
 .
.
Observe that
 .
.
We find two factors of 2 that adds up to
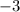 . These are,
. These are,
 .
.
Now let us split the middle term. to obtain;
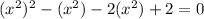
We can factor to get,
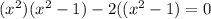
We factor further to obtain;
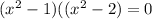

Hence the zeroes of
 are;
are;

b) To find the line tangent, we must first, find the slope using differentiation. That is,
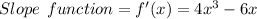
At
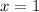 ,
,

Also, we need to determine the
 value at
value at
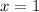 . That is;
. That is;
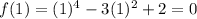
Now we can use the slope
 and the point
and the point
 to write ythe equation of the line tangent.
to write ythe equation of the line tangent.
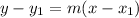
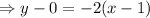
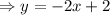
c)
If the line tangent is parallel to the line
 , then
, then
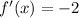
Since parallel lines have the same slope.
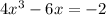
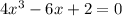
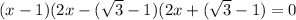
Hence the x-coordinates are,