Question

Jules kicks a soccer ball off the ground and into the air with an initial velocity of 25 feet per second. Assume the starting height of the ball is 0 feet. Approximately what maximum height does the soccer ball reach?

0.8 ft

1.6 ft

9.8 ft

19.6 ft

Approximately, how long does it take until the soccer ball hits the ground again?

0.6 sec

0.8 sec

1.6 secs

2.8 secs

Answer 1

9.8 ft for the maximum height

1.6 sec for the time it’ll take for the ball to hit the ground again

I just took a test and it shows me what I got wrong alongside the correct answers. And this was a question it asked.

Answer 2

Maximum height=9.8 ft and Time taken by soccer ball will be 0.8 secs

Explanation:

Since, the ball kicked will take the motion of projectile, therefore using the equation: h(t)=
`at^(2) +vt+d`, where h(t) is the height of the soccer ball, a is the acceleration whose value is -16 ft/sec^2 and v= 35 feet and d is the starting height which is equal to zero.

Therefore, h(t)=
`at^(2) +vt+d` (1)

Differentiating this equation with respect to t,

`h^(')(t)`=
`2at+v`

`0` =
`2(-16)t+25`

`32t`=
`25`

`t= 0.781sec`

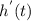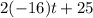
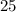
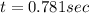
Substituting the value of t in equation (1),

`h(t)=-16(0.781)^(2) +25(0.781)`

=
`(-16)(0.609)+19.525`

=
`9.766`

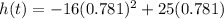
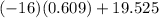
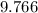
≈9.8ft

Hence, option C is correct.

Now, In order to determine the time taken until the soccer ball hits the ground, we take the equation:

`h(t)= at^(2) +vt+d`

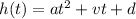
Since, when the ball hits the ground, the height will become equal to zero, therefore we have, h(t)=0

Now,
`h(t)= at^(2) +vt+d`

`0= -32.174t^(2) +25t`

`0=t(-32.174t+25)`

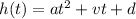
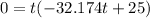
Then, one solution is t=0 and the other is:
`0=-32.174t+25`

`32t=25`

`t=(25)/(32.174)`

`t=0.777 sec`

`t`≈
`0.8 sec`

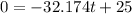
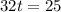
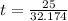
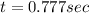
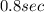
Hence, option B is correct.