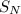Question

If the width and height of a rectangular prism are each shrunk to one seventh of the original size but the length remains the same, what is the formula to find the modified surface area?

Answer 1

The answer is
`S_N=(2)/(7)*(L*H+L*W+(W*H)/(7))`

Explanation:

In order to determine the formula, we have to know the expression of the volume of a rectangular prism.

I have attached an image that shows two formulas about the rectangular prism.

Therefore, using the same notation of the image:

L=length of the rectangular prism

W=width of the rectangular prism

H=height of the rectangular prism

So, the original surface area is:

`S_o=2*L*H+2*L*W+2*W*H`

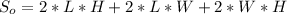
Then, if the width and height of the rectangular prism are each shrunk to one seventh of the original size but the length remains the same, the new surface area is:

`S_N=2*L*(H)/(7)+2*L*(W)/(7)+2*(W)/(7)*(H)/(7)\\S_N=(2)/(7)*(L*H+L*W+(W*H)/(7))`

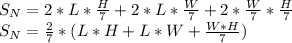
Finally, the formula of the modified surface area is
`S_N`

Answer 2

So the question ask to calculate the function or the formula that could be the solution if the width and height of a rectangular prism are shrunk to one seventh and the length stays the same, base on that, I would say that the surface area would be 2 ( 1/7w1/7h + l1/7w + l1/7h)