Question

The total number of fungal spores can be found using an infinite geometric series where a1 = 8 and the common ratio is 4. Find the sum of this infinite series that will be the upper limit of the fungal spores.

Answer 1

This infinite geometric series is divergent and thus we cannot find the sum. The sum is infinity.

Explanation:

There are two types of geometric series: convergent and divergent.

The sum of an infinite geometric sequence is given by the formula:

Sum =
`(a)/(1-r)`

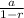
Where,

r is the common ratio and

`|r|<1`

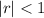
If absolute value of r is NOT less than 1, then the series is divergent and sum cannot be found.

For our given problem,
`r=4` , clearly
`|4|=4` , which is NOT less than 1, so the series is divergent and sum cannot be found.

Answer 2

The formula for infinite geometric series is equal to a1 / (1-r) where in this problem a1 is equal to 8 and r is equal to 4. In this case, r is not equal to less than 1. This means the sum should be infinity and cannot be determined definitely.