To solve the question, it will help to plot the points using a graphing calculator. This is shown below:
The image is a parallelogram. This means that:
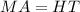
From the graph, the length of MA will be:

Using the distance formula, we can solve for the length of line MH:

We have the coordinates to be:
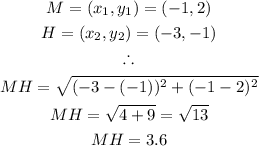
Hence, we have:
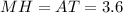
PERIMETER
The perimeter is calculated by adding all the sides. Therefore, the perimeter will be:
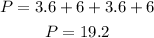
The perimeter is 19.2 units.
AREA
The area of a parallelogram is calculated using the formula:

Therefore, we have:
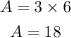
The area is 18 square units.