Question

Identify the polygon with vertices M(−1,2), A(5,2), T(3,−1), and H(−3,−1), and then find the perimeter and area of the polygon.

Answer 1

To solve the question, it will help to plot the points using a graphing calculator. This is shown below:

The image is a parallelogram. This means that:

`MA=HT`

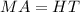
From the graph, the length of MA will be:

`\begin{gathered} MA=5-(-1)=6 \\ \therefore \\ MA=HT=6 \end{gathered}`

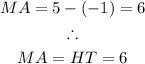
Using the distance formula, we can solve for the length of line MH:

`MH=√((x_2 - x_1)^2 + (y_2-y_1)^2)`

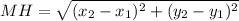
We have the coordinates to be:

`\begin{gathered} M=(x_1,y_1)=(-1,2) \\ H=(x_2,y_2)=(-3,-1) \\ \therefore \\ MH=√((-3-(-1))^2+(-1-2)^2) \\ MH=√(4+9)=√(13) \\ MH=3.6 \end{gathered}`

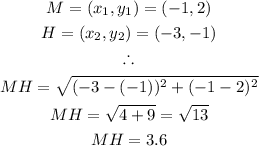
Hence, we have:

`MH=AT=3.6`

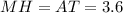
PERIMETER

The perimeter is calculated by adding all the sides. Therefore, the perimeter will be:

`\begin{gathered} P=3.6+6+3.6+6 \\ P=19.2 \end{gathered}`

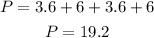
The perimeter is 19.2 units.

AREA

The area of a parallelogram is calculated using the formula:

`\begin{gathered} A=bh \\ where \\ b=HT=6 \\ h=height=3 \end{gathered}`

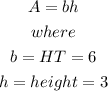
Therefore, we have:

`\begin{gathered} A=3*6 \\ A=18 \end{gathered}`

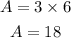
The area is 18 square units.