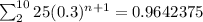Question

Evaluate the summation of 25 times 0.3 to the n plus 1 power, from n equals 2 to 10..

Answer 1

We are asked to evaluate the summation of 25 times 0.3 to the n plus 1 power, from n equals 2 to 10. In this case, we use a calculator with summation powers so as to accurately get the answer. Using a calculator, the asnwer is equal to 0.9643. 

Answer 2

`\sum_(2)^(10)25(0.3)^(n+1)=0.9642375`

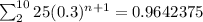
Explanation:

We have to evaluate the expression:

`\sum_(2)^(10)25(0.3)^(n+1)`

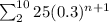
i.e. it could also be written as:

`25\sum_(2)^(10)(0.3)^(n+1)`

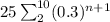
i.e. we need to evaluate:

`25[(0.3)^3+(0.3)^4+(0.3)^5+(0.3)^6+(0.3)^7+(0.3)^8+(0.3)^9+(0.3)^(10)+(0.3)^(11)]`

Hence, this could be written as:

`=25* (0.3)^3[1+0.3^1+0.3^2+0.3^3+0.3^4+0.3^5+0.3^6+0.3^7+0.3^8]`

Now, the series inside the parenthesis is a geometric series with first term as 1 and common ration as 0.3.

Hence, we could apply the summation of finite geometric series and get the answer.

We know that the sum of geometric series with n terms and common ratio less than 1 is calculated as:

`S_n=a* ((1-r^n)/(1-r))`

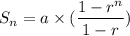
Here a=1 and r=0.3

Hence the sum of geometric series is:

`S_9=1* ((1-0.3^9)/(1-0.3))\\\\S_9=1.4285`

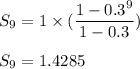
Hence, the final evaluation is:

`=25* (0.3)^3* 1.4285\\\\=0.9642375`

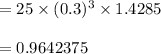
Hence,

`\sum_(2)^(10)25(0.3)^(n+1)=0.9642375`