Question

A child with a weight of 4.5 x 10^2 N sits on a seesaw 0.60 m from the axis of rotation. How far from the axis of rotation on the other side should a child with aweight of 600 N sit so the seesaw will remain balanced?

Answer 1

The given problem can be exemplified in the following diagram:

We are asked to determine the value of "x" for which the seesaw will remain balanced. To do that we will determine the torque on the axis of rotation. We will take clockwise as positive.:

`\Sigma T=(4.5*10^5N)(0.6m)-(600N)x`

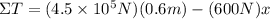
Since we want the seesaw to remain balanced, the total torque will add up to zero:

`(4.5*10^5N)(0.6m)-(600N)x=0`

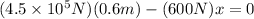
Now, we solve the products:

`270000Nm-(600N)x=0`

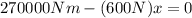
Now, we solve for "x". First, we will subtract 270000 from both sides:

`-(600N)x=-270000Nm`

Now, we divide both sides by -600:

`x=(-270000Nm)/(-600N)`

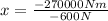
Solving the operations:

`x=450m`

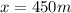
Therefore, the distance from the axis of rotation must be 450 meters.