If n is at x = 4, then we can rewrite the transformation notation as:
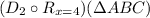
This transformation notation is read as a reflection across the line x = 4 and dilation of a scale factor of 2.
To determine the graph of the image, let's do the reflection across the line x = 4 first.
Basically, the image will be on the opposite side of the line but at the same distance from the line. See the illustration below.
Now, let's apply dilation of a scale factor of 2 on the reflection by multiplying its coordinates by 2.
A' (1, 5) → (2, 10)
B' (0, 1) → (0, 2)
C' (3, 0) → (6, 0)
Let's plot these new coordinates to the graph.
The graph of the image after the given series of transformations is shown above by the black triangle.