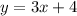To find the perpendicular bisected of the line segment whose endpoints are (3,-7) (-9,-3).
We need to things:
1. the midpoint of the given point
2. the slope
The midpoint = p
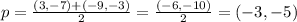
To find the slope, first we will find the slope of the line segment whose endpoints are
(3,-7) (-9,-3)
so,
Slope = m = rise/run
Rise = -3 - (-7) = 4
Run = -9 - 3 = -12
Slope =
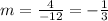
The slope of the required line = m'
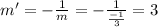
So, the equation of the line will be :
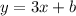
b is the y - intercept and will be calculated using the point p
when x = -3 , y = -5
so,
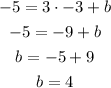
So, the equation for the perpendicular bisected is: