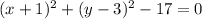Question

What is the general equation of the circle passing through (-2,7),(-2,-1), and (3,2)?

Answer 1

Using the general equation for a circle, we have:

`\begin{gathered} (x-xc)^2+(y-yc)^2-r^2=0\text{ (xc and yc are the coordianates of the center and r is the radius)} \\ (-2-xc)^2+(7-yc)^2-r^2=0\text{ (Equation for point 1)} \\ (-2-xc)^2+(-1-yc)^2-r^2=0\text{ (Equation for point 2)} \\ (3-xc)^2+(2-yc)^2-r^2=0\text{ (Equation for point 3)} \end{gathered}`

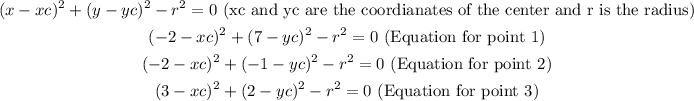
Then, we are going to subtract the first equation from the second and the first from the third to get a system of equations. Doing so, we have:

`\begin{gathered} (-2-xc)^2+(-1-yc)^2-r^2-((-2-xc)^2+(7-yc)^2-r^2)=0\text{ } \\ 4+4xc+(xc)^2+1+2yc+(yc)^2-r^2-(4+4xc+(xc)^2+49-14yc+(yc)^2-r^2)=0 \\ 4+4xc+(xc)^2+1+2yc+(yc)^2-r^2-4-4xc-(xc)^2-49+14yc-(yc)^2+r^2=0 \\ -48+16yc=0\text{ (Adding like terms)} \\ 16yc=48\text{ (Adding 48 to both sides of the equation)} \\ yc=3\text{ (Dividing the equation by 3 on both sides)} \end{gathered}`
`\begin{gathered} (3-xc)^2+(2-yc)^2-r^2-((-2-xc)^2+(7-yc)^2-r^2)=0\text{ } \\ 9-6xc+(xc)^2+4-4yc+(yc)^2-r^2-(4+4xc+(xc)^2+49-14yc+(yc)^2-r^2)=0 \\ 9-6xc+(xc)^2+4-4yc+(yc)^2-r^2-4-4xc-(xc)^2-49+14yc-(yc)^2+r^2=0 \\ -40-10xc+10yc=0\text{ (Adding like terms)} \\ -40-10xc+10(3)=0\text{ (Replacing yc=3)} \\ -40-10xc+30=0(\text{ Multiplying)} \\ -10-10xc=0\text{ (Subracting like terms)} \\ -10xc=10\text{ (Adding 10 to both sides of the equation)} \\ xc=-1 \end{gathered}`

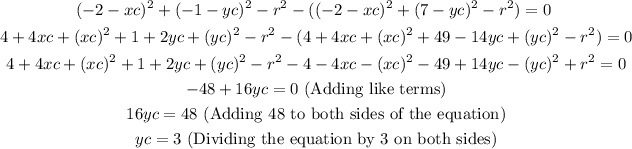
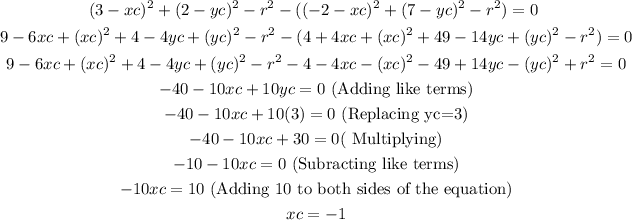
We found that the coordinates of the center are (-1,3), Replacing them in the first equation to find the radius, we have:

`\begin{gathered} (-2-(-1))^2+(7-3)^2-r^2=0\text{ (Replacing the values)} \\ (-2+1))^2+(7-3)^2-r^2=0\text{ (Using the sign rules)} \\ (-1)^2+(4)^2=r^2(\text{ Subtracting and adding r}^2\text{ to both sides of the equation)} \\ 1+16=r^2\text{ (Raising the numbers to the power of 2)} \\ 17=r^2\text{ (Adding)} \\ 4.12=r\text{ (Taking the square root)} \end{gathered}`

Knowing that the center is at (-1,3) and the radius is 4.12, the general equation would be:

`(x+1)^2+(y-3)^2-17=0`