Question

The following sample of n = 4 scores was obtainedfrom a population with unknown parameters. Scores:2, 2, 6, 2a. Compute the sample mean and standard deviation.(Note that these are descriptive values that sum-marize the sample data.)b. Compute the estimated standard error for M. (Notethat this is an inferential value that describes howaccurately the sample mean represents the un-known population mean.)

Answer 1

a) The sample mean is given by the formula below

`\begin{gathered} \mu_x=\frac{\sum_i^\text{ }x_i}{N} \\ x_i\rightarrow\text{ elements in the sample} \\ N\rightarrow\text{ sample size} \end{gathered}`

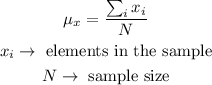
Therefore, in our case,

`\begin{gathered} \mu_x=(2+2+6+2)/(4)=(12)/(4)=3 \\ \Rightarrow\mu_x=3 \end{gathered}`

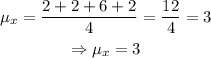
On the other hand, the sample standard deviation is

`s=\frac{\sqrt{\sum_i^{\text{ }}(x_i-\mu_x)^2}}{√(n-1)}`

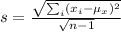
Thus, in the case of the given sample,

`\begin{gathered} s=(√((2-3)^2+(2-3)^2+(6-3)^2+(2-3)^2))/(√(4-1)) \\ \Rightarrow s=(√(1+1+9+1))/(√(3))=\sqrt{(12)/(3)}=√(4)=2 \\ \Rightarrow s=2 \end{gathered}`

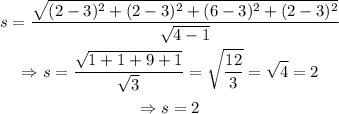
The sample mean is 3 and the sample standard deviation is 2.

b) The estimated standard error of the mean is given by the formula below

`SE=(s)/(√(n))`

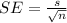
Hence, in our case,

`\Rightarrow SE=(2)/(√(4))=1`

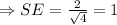
The estimated standard error for the mean is equal to 1.