Answer:
a) The velocity of the rock during ascent at 180 meters above the surface is approximately 17.799 meters per second.
b) The height of the rock from the ground is 219 meters from the ground.
Step-by-step explanation:
a) The rock experiments a free fall, in which this element is projected upwards, decelerated until rest is reached and then it falls down. Please notice that free fall is a case of uniformly accelerated motion, in which object is accelerated by gravity. The velocity of the rock is described by the following kinematic equation:
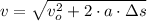 (1)
(1)
Where:
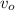 - Initial velocity, measured in meters per second.
- Initial velocity, measured in meters per second.
 - Final velocity, measured in meters per second.
- Final velocity, measured in meters per second.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
 - Travelled distance, measured in meters.
- Travelled distance, measured in meters.
If we know that
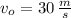 ,
,
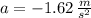 and
and
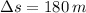 , then the velocity during ascent at 180 meters is:
, then the velocity during ascent at 180 meters is:
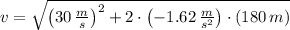
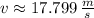
The velocity of the rock during ascent at 180 meters above the surface is approximately 17.799 meters per second.
b) The height of the rock is calculated from this kinematic formula:
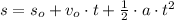 (2)
(2)
Where:
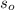 - Initial position of the rock, measured in meters.
- Initial position of the rock, measured in meters.
 - Final position of the rock, measured in meters.
- Final position of the rock, measured in meters.
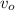 - Initial velocity of the rock, measured in meters per second.
- Initial velocity of the rock, measured in meters per second.
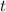 - Time, measured in seconds.
- Time, measured in seconds.
 - Acceleration, measured in meters per square second.
- Acceleration, measured in meters per square second.
If we know that
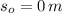 ,
,
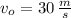 ,
,
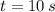 and
and
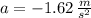 , then the height of the rock from the ground is:
, then the height of the rock from the ground is:
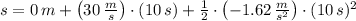
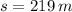
The height of the rock from the ground is 219 meters from the ground.