Question

Find the rate of change of A with respect to h if r remains constant in A=2pir(r+h)

Answer 1

The rate of change describes how one quantity changes with respect to the other.

When you have a linear function (given by y=mx+b), where m is the slope and b is the y-intercept, the slope will be the rate of change m.

Now, you have the function:

`A=2\pi r(r+h)`

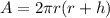
You can take it to the general form y=mx+b, as follows:

`\begin{gathered} A=2\pi r(r+h) \\ A=2\pi r^2+2\pi r\cdot h \end{gathered}`

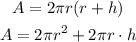
The problem says r is a constant, then the term 2pir^2 is a constant, it will be the b in the general form of the function. A will be the y-term, h will be the x-term, and finally, 2pir will be the slope m.

`\begin{gathered} y=mx+b \\ A=2\pi r\cdot h+2\pi r^2 \end{gathered}`

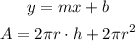
Knowing that the rate of change is the slope, then the answer is: The rate of change is 2pir