Question

Please help me due today!!

please only answer if you know.

questions 1-4
​

Answer 1

Explanation:

From the given equations of the function,

1). f(x) = x² + 4x + 3

= x² + 2(2x) + 4 - 1

f(x) = (x + 2)² - 1

This is in the vertex form of a parabola [y = (x - h)² + k]

Here, (h, k) is the vertex of the parabola.

By comparing both the equations of the parabola,

(-2, 1) will be the vertex.

Table for input - output values,

x intercepts → (x + 2)² + 1 = 0

(x + 2) = ±1

x = -2 ± 1

x = -3, -1

Line of symmetry → x = -3

y-intercept of the graph, x = 0

y = (0 + 2)²- 1

= 4 - 1

y = 3

2). f(x) = x² - 6x + 11

= x² - 2(3x) + 9 + 2

= (x - 3)² + 2

By comparing the equation of the function with the vertex form of the parabola,

(3, -2) is the vertex.

Line of symmetry → x = 3

x-intercept → (x - 3)² + 2 = 0

(x - 3) = ±√(-2)

x = 3 ± √(-2) [Imaginary number]

Therefore, NO y-intercept.

y-intercept → y = 0 - 6(0) + 11 = 11

3). f(x) = -x² + 2x - 2

= -[x² - 2x + 2]

= -[x² - 2(1.x) + 1 - 1] - 2

= -[(x - 1)²- 1] - 2

= -(x - 1)²- 1

By comparing this equation with the vertex form of the equation,

(1, -1) is the vertex.

x - intercepts → y = -(x - 1)²- 1 = 0

(x - 1) = ±√(-1)

x = 1 ± √(-1) [Imaginary numbers]

Therefore, no x-intercepts.

y-intercept → y = -(0 - 1)² + 3

y = 2

4). y =
`(1)/(2)x^(2)-4x+5`

y =
`(1)/(2)(x^(2)-8x+10)`

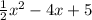
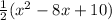
y =
`(1)/(2)[x^(2)-2(4x)+10]`

y =
`(1)/(2)[x^(2)-2(4x)+16-6]`

y =
`(1)/(2)[(x-4)^2-6]`

y =
`(1)/(2)(x-4)^2-3`

Vertex → (4, -3)

Line of symmetry → x = 4

x - intercepts → x = 4 ± √6

x = 1.55, 6.45

y - intercepts → y = 5