(0,15)
1) Since the g(x) function has x-intercepts "5" and "-1" then we can write the quadratic factored form:
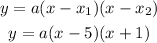
2) Since we were told that this g(x) function has been reflected over the x-axis and stretched vertically by a factor of 3, we can rewrite that "a" coefficient that way:
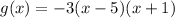
3) So, let's expand that to get the function and the y-intercept:
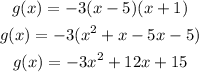
Note that the minus sign in the leading coefficient points out that the equation has been vertically stretched and reflected in comparison to the parent function.
Thus, the y-intercept of g(x) is (0,15)