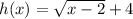Question

The graph of f (in blue) is translated a whole number of units horizontally and vertically to obtain the graph of h(in red).

The function f is defined by f(x) = square root of x
Write down the expression for h(x).

Please help!

Answer 1

h(x) = square root of (x-2) +4

Answer 2

`h(x)=√(x-2)+4`

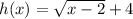
Explanation:

Initially the graph f (x) is shifted horizontally to the right.

When the graph shifts to right the function then becomes

f(x)→f(x-b)

Where b is the units by which it is shifted towards right .

So, in the figure we can see that it is shifted 2 units to the right .

So, f(x)→f(x-2)

Since f(x) is
`√(x)`

So, f(x-2) =
`√(x-2)`

Now the new obtained graph is again shifted vertically upward

When the graphs shifts upward f(x) →f(x)+b

where b is the units by which it is shifted upward

So, our obtained f(x-2) when shifted upward by 4 units so using the above given transformation of upward shift i.e. f(x) →f(x)+b

So, Our new graph h(x) = f(x-2)+4

⇒
`h(x)=√(x-2)+4`