Answer:
1. 9 inches, 12 inches and 15 inches
2. 54 square inches
Explanation:
1. The first part of this question would lead to a quadratic equation. Let the shorter leg be represented by x.
shorter leg = x
other leg = x + 3
hypotenuse = 15 inches
Applying the Pythagoras theorem, we have;
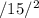 =
=
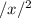 +
+

225 =
 +
+
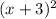
225 =
 +
+
 + 6x + 9
+ 6x + 9
= 2
 + 6x + 9
+ 6x + 9
2
 + 6x + 9 - 225 = 0
+ 6x + 9 - 225 = 0
2
 + 6x - 216 = 0
+ 6x - 216 = 0
divide through by 2 to have
 + 3x - 108 = 0
+ 3x - 108 = 0
From the quadratic formula;
x = (-b ±
 ) ÷ 2a
) ÷ 2a
but, a = 1, b = 3, c = -108
x = (-3 ±
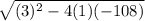 ) ÷ 2
) ÷ 2
= (-3 ±
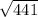 ) ÷ 2
) ÷ 2
= (-3 ± 21) ÷ 2
Thus,
x = (-3 + 21) ÷ 2 OR x = (-3 - 21) ÷ 2
x = 9 OR x = -12
So that, x = 9 inches
The shorter leg is 9 inches, and the other leg is 12 inches.
2. The area of the triangle can be determined by applying Heron's formula:
A =
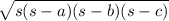
where s is the average value of the sum of the three sides a, b, and c.
Let, a = 9, b = 12 and c = 15
s =
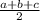
=
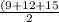
= 18
A =
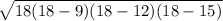
=
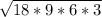
=
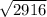
A = 54
Area of the triangle is 54 square inches.