Question

The annual number of units demanded, x, of a product (in thousands) by consumers at unit price p, in dollars per unit, is modeled by the formula P^2 + x = 8 X explicitly as a function of p: X = 8 - p^2 a. What is the practical domain of the function? B. How many units will be sold at a unit price of $0.9? ______ units C. At what price is/are 1868 units sold? $________

Answer 1

`\begin{gathered} a)p\leq2\sqrt[]{2} \\ b)7\text{units} \\ c)$\$2.48$ \end{gathered}`

Explanations:

Given the annual number of units demanded, x, of a product (in thousands) by consumers at unit price p, in dollars per unit, is modeled by the formula;

`p^2+x=8`

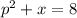
Given that the number of units x as a function of p is expressed as:

`x=8-p^2`

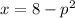
a) The practical domain of the function is the value of the unit price "p" for which the function exists.

Since the annual number of units demanded "p" cannot be negative, hence the domain exists at the point where:

`\begin{gathered} 8-p^2\ge0 \\ 8\ge p^2 \\ p^2\leq8 \\ p\leq\sqrt[]{8} \\ p\leq2\sqrt[]{2}\text{ (Domain)} \end{gathered}`

b) In order to get the number of units that will be sold at a unit price of $0.9, you will substitute p = 0.9 into the function and calculate the value of x as shown:

`\begin{gathered} x=8-p^2 \\ x=8-(0.9)^2 \\ x=8-0.81 \\ x=7.19 \\ x\approx7 \end{gathered}`

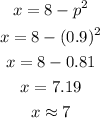
This shows that about 7 units will be sold at a unit price of $0.9

c) In order to get the price for 1868 units that were sold, you will substitute X = 1868 into the given expression as shown:

`\begin{gathered} x=8-p^2 \\ 1.868=8-p^2 \\ 1.868-8=-p^2 \\ p^2=8-1.868 \\ p^2=6.132 \\ p=\sqrt[]{6.132} \\ p=2.4763 \end{gathered}`

Therefore the price at which 1868 units is sold is about $2.48