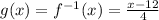Question

If g(x) is the inverse of f(x)=4x+12 and f(x)=, what is g(x)

Answer 1

Hello,
f(x)=y=4x+12

x=4y+12
==>4y=x-12
==>y=x/12- 3

g(x)=x/12 -3

Answer 2

`f^(-1)(x)=g(x)=(x-12)/(4)`

Explanation:

The problem tell us that
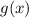`g(x)` is the inverse of
`f(x)`, where:

`f(x)=4x+12`

So, we need to find the inverse function of
`f(x)` in order to find
`g(x)`

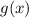
Let's find the inverse function using the following steps:

1. Replace
`f(x)` with
`y`:

`f(x)=y=4x+12`

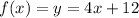
2. Solve the equation for
`x`:

`(y-12)/(4) =x`

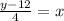
3. Replace every
`x` with a
`y` and replace every
`y` with a
`x`:

`y=(x-12)/(4)`

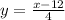
4. Finally, replace
`y` with
`f^(-1)(x)`

`f^(-1)(x)=(x-12)/(4)`

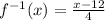
Therefore:

`g(x)=f^(-1)(x)=(x-12)/(4)`