Question

Question Attached as Screenshot Below:Only Question 2:This is NOT a test

Answer 1

We must compute the derivative of the function at x = 2:

`f(x)=4.5x^2-3x+2,`

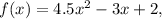
using the limit definition.

1) We write explicitly the derivative as a limit:

`f^(\prime)(2)=\lim _(x\rightarrow2)(f(x)-f(2))/(x-2)=\lim _(x\rightarrow2)((4.5x^2-3x+2)-(4.5\cdot2^2-3\cdot2+2))/(x-2)\text{.}`

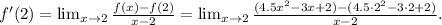
2) We simplify the expression above:

`f^(\prime)(2)=\lim _(x\rightarrow2)((4.5x^2-3x+2)-14)/(x-2)=\lim _(x\rightarrow2)(4.5x^2-3x-12)/(x-2)\text{.}`

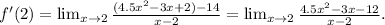
If we replace x by 2, we get a 0 in the numerator and denominator. So this is a limit of the type 0/0 where we can apply L'Hopital's rule.

3) We apply L'Hopital's rule, which consists of taking the derivative of numerator and denominator, we get:

`f^(\prime)(2)=\lim _(x\rightarrow2)\frac{4.5\cdot2x^{}-3}{1}\text{.}`

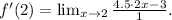
4) Now, we see that there is no problem to replace x by 2, doing that we get:

`f^(\prime)(2)=4.5\cdot2\cdot2-3=15.`

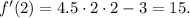
Answer: f'(2) = 15