Question

If a polynomial function f(x) has roots 4-13i and 5, the factor of f(x) must be_______.

a. (x+(13-4i))
b. (x-(13+4i))
c. (x+(4+13i))
d. (x-(4+13i))

Answer 1

So the problem ask to choose among the following choices that has the factor of f(x) if a polynomial function f(x) has a roots 4-13i and 5, base on that, the answer is not in the choices, base on my computation, the answer is f(x) = (x-y+13i)(x-5), I hope you are satisfied with my answer 

Answer 2

Answer: Option 'D' is correct.

Explanation:

Since we have given that

If a polynomial function f(x) has 2 two roots are as follows:

1) 4-13i

2)5

So, the factors of f(x) must be in the form of

`(x-\alpha)(x-\beta)\\\\here,\ \alpha\ and\ \beta\text{ are two roots}`

Since it has one complex roots so, it will also have one conjugate root of this complex root:

`\alpha=4-13i\\\\\bar{\alpha}=4+13i`

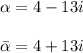
so, one of the factor of f(x) must be

`(x-(4+13i))`

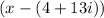
Hence, Option 'D' is correct.