Question

A population of bacteria is treated with an antibiotic. It is estimated that 5,000 live bacteria existed in the sample before treatment. After each day of treatment, 40% of the sample remains alive. Which best describes the graph of the function that represents the number of live bacteria after x days of treatment?

A. f(x) = 5000(0.4)x, with a horizontal asymptote of y = 0

B. f(x) = 5000(0.6)x, with a vertical asymptote of x = 0

C. f(x) = 5000(1.4)x, with a horizontal asymptote of y = 0

D. f(x) = 5000(1.6)x, with a vertical asymptote of x = 0

Answer 1

The correct option is A.

Step by step explanation:

The exponential function is defined as

`f(x)=ab^x`

Where, a is initial value and b is growth factor or decay factor.

The initial population of bacteria is 5000.

After each day of treatment, 40% of the sample remains alive. It means the growth factor or decay factor is

`(40)/(100)=0.4`

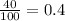
Therefore the required function is

`f(x)=5000(0.4)^x`

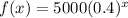
The horizontal asymptote is y=0 because

`f(x)\rightarrow 0\text{ as }x\rightarrow\infty`

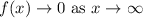
Therefore option A is correct.

Answer 2

"f(x) = 5000(0.4)x, with a horizontal asymptote of y = 0" is the one among the following choices given in the question that best describes the graph of the function that represents the number of live bacteria after x days of treatment. The correct option among all the options that are given in the question is the first option or option "A".