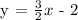Question

Write an equation of the line in slope-intercept form (2,1) (0,-2)

Answer 1

Given the following coordinates of the two points that pass through the line.

Point 1 : 0, - 2

Point 2 : 2, 1

Let's determine the equation of the line:

Step 1: Let's determine the slope (m).

`\text{ Slope = m = }(y_2-y_1)/(x_2-x_1)\text{ = }\frac{1\text{ - (-2)}}{2\text{ - 0}}`
`\text{ m = }\frac{1\text{ + 2}}{2}\text{ = }(3)/(2)`

Step 2: Let's determine the y - intercept (b). Using the slope-intercept form: y = mx + b, plug in m = 3/2 and x,y = 0, -2.

`\text{ y = mx + b}`
`\text{ -2 = (}(3)/(2))(0)\text{ + b}`
`\text{ b = -2}`

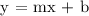
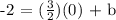
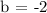
Step 3: Let's complete the equation. Plug in m = 3/2 and b = -2 in y = mx + b.

`\text{ y = mx + b}`
`\text{ y = (}(3)/(2))x\text{ + (-2)}`
`\text{ y = }(3)/(2)x\text{ - 2}`

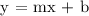
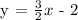
Therefore, the equation of the line is:

`\text{ y = }(3)/(2)x\text{ - 2}`