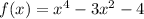Answer:

Explanation:
Complex Conjugate Root Theorem-
If
 is a root of a polynomial P with a and b real numbers, then its complex conjugate
is a root of a polynomial P with a and b real numbers, then its complex conjugate
 is also a root of P.
is also a root of P.
So, all roots of the polynomial function are
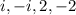
Hence, the function will be,
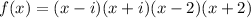
![=[(x-i)(x+i)]\cdot[(x-2)(x+2)]](https://img.qammunity.org/2017/formulas/biology/high-school/sizn5al8t21dpqu2d4wrrgmuzktwxg92fz.png)
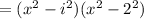
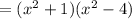
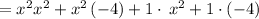
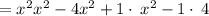
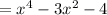
The leading coefficient in this case is 1, so the function is,