Answer:
Explanation:
The volume of the solid is the area of the front face multiplied by the length.
The front face of the solid has the shape of a right triangle.
The leftmost side of that triangle is unknown.
We can use Pythagoras's theorem to find the length of the leftmost side.
The length of the leftmost side is
![\begin{gathered} L=\sqrt[]{20.5^2-13.3^2} \\ L=15.6 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xcenraaaz7rozau01aad.png)
therefore, the volume of the solid is
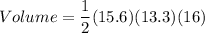
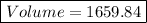
The surface area of the solid is the sum if the surface areas of all its sides.
Surface area is
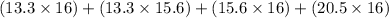
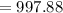
Hence, the area of the solid is 997.88 square mm.