Question

a random sample of 130 students is chosen from a population of 4,500 students. if the mean iq in the sample is 120 with a standard deviation of 5, what is the 99% confidence interval for the students' mean iq score? answers given below: 118.87−121.13 107.12−132.88 125−135 115−125

Answer 1

`C.I.=120 \pm z_( \alpha /2) ( \sigma )/( √(n) ) \\ =120 \pm 2.58 * (5)/( √(130) ) \\ =120 \pm 1.13 \\ =118.87 - 121.13`

Answer 2

Answer with explanation:

Total Sample Size = 4,500 Students

Sample Chosen(n) = 130 students

Mean IQ of the Sample,
`\bar{X} = 120`

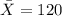
Standard Deviation,
`\sigma=5`

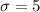
To Calculate 99% confidence interval for the students' mean IQ score, we will calculate,

`Z_(99 percent)=2.58`

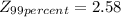
Formula for Confidence Interval

`=\bar{X} \pm Z_(99 percent)* (\sigma)/(√(n))\\\\=120 \pm 2.58 * (5)/(√(130))\\\\=120 \pm (12.9)/(11.401)\\\\ =120 \pm 1.1314\\\\=120 \pm 1.13`

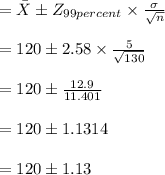
The Value of Confidence interval will lie between

⇒ 120 - 1.13 to 120 +1.13

⇒118.87 to 121.13

Option A: 118.87−121.13