Question

The sum of two numbers is 62, and their difference is 12. What are the numbers?

Answer 1

x+y=62 ; x-y=12 Solve for x in one equation and plug that value into the other equation. ===> x=12+y ; 12+y+y=62 Subtract 12 to both sides (2y=50), then divide by 2 to find y (y=25). Now, plug 25 as y into x=12+y, getting x=37. Your two numbers are 37 and 25.

Answer 2

Answer: The required numbers are 37 and 25.

Step-by-step explanation: Given that the sum of two numbers is 62 and their difference is 12.

We are to find the numbers.

Let x and y represents he given numbers.

Then, according to the given information, we have

`x+y=62~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)\\\\x-y=12~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

Adding equations (i) and (ii), we get

`(x+y)+(x-y)=62+12\\\\\Rightarrow 2x=74\\\\\Rightarrow x=(74)/(2)\\\\\Rightarrow x=37.`

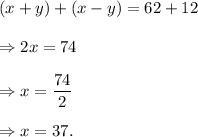
And, from equation (i), we get

`37+y=62\\\\\Rightarrow y=62-37\\\\\Rightarrow y=25.`

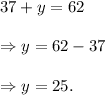
Thus, the required numbers are 37 and 25.