Question

(PLEASE HELP)

(solve using substitution


There are a total of 64 students in a drama club and a year yearbook club. The drama club has 10 more students than the yearbook club.

A. Write the system of linear equations that represents this situation. let x represent the number of students in the drama club and y represents the number of students in the yearbook club.

(fill in the blanks)

System of equations: x= ___

___x + ___y = 64 d

B. How many students are in the drama club? The yearbook club?

There are __ students in the drama club.

There are __ students in the yearbook club

Answer 1

x=y+10

1x+1y=64 d

y=27 year book club

x=37 drama club

Explanation:

x=y+10

1x+1y=64 d

y+10+y=64

2y+10=64

2y=54

y=27

x=37

Answer 2

Part A)

`x=10+y\\\\ x+y=64`

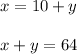
Part B)

There are 37 students in the drama club.

And there are 27 students in the yearbook club.

Explanation:

We know that there are 64 students in total in a drama and yearbook club.

The drama club has 10 more students than the yearbook club.

We will let x represent the number of students in the drama club and y represent the number of students in the yearbook club.

Part A)

Since the drama club (x) has 10 more students than however many the yearbook club (y) has, we can write:

`x=10+y\\`

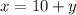
And since there are in total 64 students, x plus y must equal that sum. So:

`x+y=64`

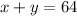
Part B)

We can substitute the first equation into the second:

`(10+y)+y=64`

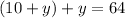
Combine like terms:

`2y+10=64`

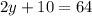
Subtracting 10 from both sides:

`2y=54`

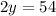
Dividing by 2:

`y=27`

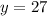
So, the amount of students in y or the yearbook club is 27 students.

Since the drama club has 10 more, there are 37 students in the drama club.