Question

Finding the mean, mode, median, mode and outlier of data 45,69,72,76,78, 88,90, 96, 119, 145See rest of info from photo

Answer 1

The mean of the data is;

`\bar{x}=87.8`

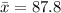
The median of the given data is;

The data set has no Mode

The outliers of the given data can be 45 and 145 because they are very far away from the mean of the data.

Step-by-step explanation:

Given the data values;

The mean of the data is;

`\begin{gathered} \bar{x}=(45+69+72+76+78+88+90+96+119+145)/(10) \\ \bar{x}=(878)/(10) \\ \bar{x}=87.8 \end{gathered}`

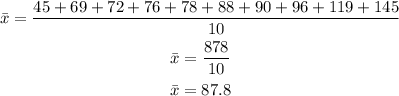
The median of the given data is;

For the mode, we can observe that all the data values have equal frequency (they all appear only once).

Therefore, the data set has no Mode

The outliers are the data set that is much larger or much lower than all the other data values.

The outliers of the given data can be 45 and 145 because they are very far away from the mean of the data.