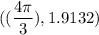Step 1
Critical points on the graph of a function where the derivative is zero or the derivative does not exist are important to consider in many application problems of the derivative. The point ( x, f(x)) is called a critical point of f(x) if x is in the domain of the function and either f′(x) = 0 or f′(x) does not exist.
Step 2
Find f'(x)
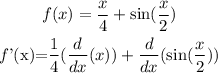
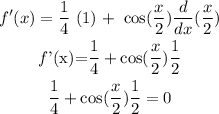
But for the critical point f'(x)=0
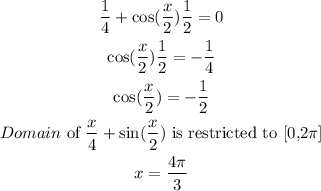
Hence;
![\begin{gathered} f((4\pi)/(3))=((4\pi)/(3))/(4)+\sin (((4\pi)/(3))/(2)) \\ f((4\pi)/(3))=(1)/(3)\pi+\frac{\sqrt[]{3}}{2}=1.913222955 \\ f((4\pi)/(3))\approx1.9132\text{ to 4 decimal places} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/n5cpd86onjk9uepbwhjz.png)
Hence, the critical points will be;