Question

The vertices of a polygon are P(0,4), Q(5,4), R(5,−3) and S(0,−3). What is

the perimeter of the polygon?

Answer 1

Perimeter of the polygon p = 24

Explanation:

Step(i):-

Given the vertices of a polygon are

P(0,4) ,Q( 5,4) ,R( 5,-3) and S(0,-3)

The distance of PQ

`a = PQ = \sqrt{(4-4)^(2) +(5-0)^(2) } = √(25) =5`

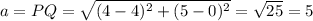
The distance of QR

`b = Q R= \sqrt{(-3-4)^(2) +(5-5)^(2) } = √(49) =7`

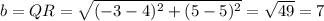
The distance of RS

`c = RS = \sqrt{(0-5)^(2) +(-3+3)^(2) } = √(25) =5`

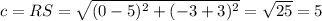
The distance of PS

`d = PS = \sqrt{(0-0)^(2) +(-3-4)^(2) } = √(49) =7`

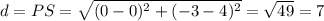
Step(ii):-

Perimeter of the polygon

= sum of all sides of polygon

p = a+ b+ c+ d

p = 5+7+5+7

p = 24

Final answer:-

Perimeter of the polygon p = 24